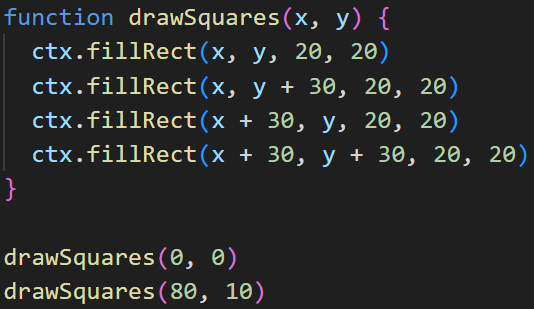
In programming, we usually don't want to write the same lines of code over and over. That's why we use functions. With a function or procedure, we can keep "calling" that function to repeat the contents. Try it:

As long as we have the function defined, we can call it anywhere, even inside another function:

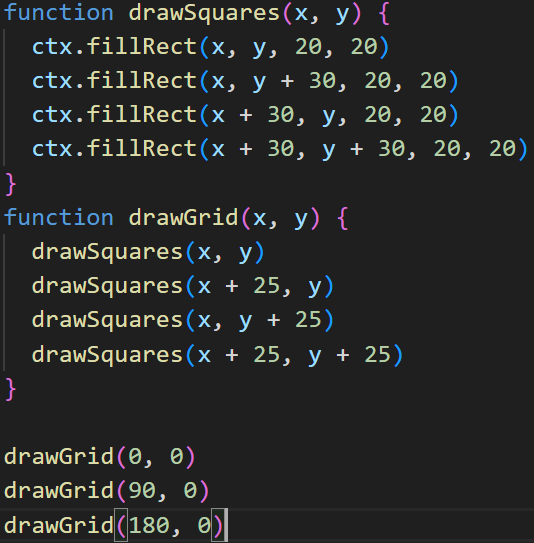
In this example, the drawGrid procedure is waiting on the drawSquares procedure - which itself is waiting on the fillRect function. In terms of memory, the stack is the place in memory where the current procedures are stored. Just like any other form of memory, the stack can run out of space. If unaddressed, this might result in other memory getting overwritten and all sorts of errors, called a stack overflow. Luckily, most computers have ways of detecting when the stack is overflowing and stops the program.

So what happens if a function is called inside its own definition? Well, usually, the stack will just get bigger and bigger, simply storing the same data in the stack over and over, until it overflows.

However, if we use selection to only sometimes call the function, we can get working code! This is called recursion.

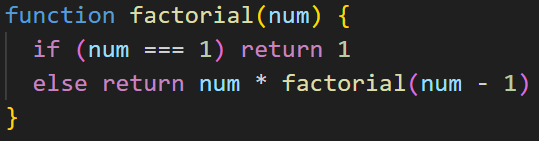
Here's an example of a recursive function:

Recursion is often the most efficient way to solve programming problems, but it's not easy to work with. The most famous use of recursion is in a factorial function, which returns the product of all the integers from 1 to the input. Have a go at trying different inputs into the factorial function.

Input:

Output:

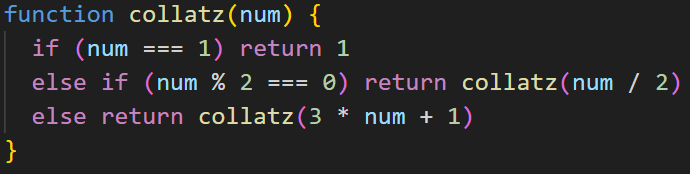
You might have noticed that if you try any values other than positive integers, it won't work. Internally, this has caused a stack overflow because the base case, 1, is never used as an argument. It's not always easy to be sure whether the base case will ever be reached. For example, the following code divides the input by 2 if even, and multiplies by 3 and adds 1 if odd, repeating until it reaches the base case 1.

Input:

Output:

You might think that it always ends up returning 1 for positive integers. And mathematically, you might be correct - it's an unsolved problem. But if you enter, say, 670617279, too much recursion is required to reach the final answer, so it throws an error. For this kind of reason, recursion is most useful when you have a good idea of how deep the function will go. For more info on recursion click here.